What Is 5 to the Power of 0
Exponents Calculator or e estimator is used in solving exponential forms of expressions. Information technology is also known as raised to the power figurer.
Properties of exponents figurer:
This reckoner solves bases with both negative exponents and positive exponents. It also provides a step by step method with an accurate answer.
What is an exponent?
An exponent is a small-scale number located in the upper, correct-hand position of an exponential expression (base exponent), which indicates the power to which the base of the expression is raised.
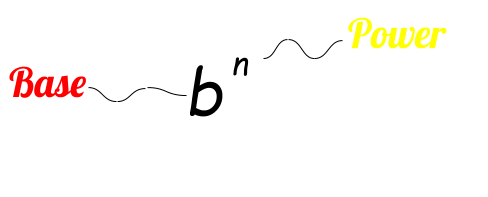
The exponent of a number shows y'all how many times the number is to be used in a multiplication. Exponents do non have to be numbers or constants; they can be variables.
They are often positive whole numbers, but they can exist negative numbers, partial numbers, irrational numbers, or complex numbers. Information technology is written as a modest number to the correct and above the base number.
Types:
In that location are basically ii types of exponents.
-
Positive exponent
A positive exponent tells how many times a number is needed to be multiplied past itself. Use our exponent estimator to solve your questions.
-
Negative exponent
A negative exponent represents which fraction of the base, the solution is. To simplify exponents with power in the form of fractions, employ our exponent calculator.
Example:
Calculate the exponent for the 3 raised to the power of 4 (3 to the power of iv).
It means = 34
Solution:
three*3*3*three = 81
4 to the tertiary power = 81
Therefore the exponent is 81
two raised to the power calculator.
Example:
What is the value of exponent for 2 enhance to power 9 (2 to the 9th power)
It means = two9
Solution:
2*ii*2*two*two*2*two*2*2 = 512
2 to the 9th ability = 512
Therefore the exponent is 512.
Example :
How do yous calculate the exponents of 5,6,7 to the ability of 4?
It ways = v4, 64, 7four
Solution:
5*5*five*v = 625
vi*half-dozen*6*6 = 1296
7*seven*vii*7 = 2401
Therefore the exponents are 625, 1296, 2401.
How to calculate the nth power of a number?
The nth power of a base, permit's say "y", means y multiplied to itself nth fourth dimension. If nosotros are to find the fifth power of y, it is y*y*y*y*y.
Some other solutions for the nth power calculator are in the following table.
| 0.1 to the power of 3 | 0.00100 |
| 0.5 to the power of 3 | 0.12500 |
| 0.5 to the power of 4 | 0.06250 |
| 1.2 to the power of four | two.07360 |
| 1.02 to the tenth power | 1.21899 |
| i.03 to the 10th power | ane.34392 |
| ane.2 to the power of 5 | ii.48832 |
| 1.4 to the 10th ability | 28.92547 |
| 1.05 to the power of 5 | i.27628 |
| 1.05 to the 10th ability | i.62889 |
| one.06 to the tenth power | i.79085 |
| 2 to the tertiary power | 8 |
| 2 to the power of 3 | 8 |
| 2 raised to the power of 4 | 16 |
| 2 to the power of vi | 64 |
| two to the power of vii | 128 |
| 2 to the ninth power | 512 |
| 2 to the tenth ability | 1024 |
| 2 to the 15th ability | 32768 |
| 2 to the 10th power | 1024 |
| two to the power of 28 | 268435456 |
| 3 to the power of ii | ix |
| 3 to the 3 ability | 27 |
| 3 to the 4 power | 81 |
| 3 to the 8th ability | 6561 |
| iii to the 9th power | 19683 |
| three to the twelfth power | 531441 |
| three to what power equals 81 | 3four |
| 4 to the power of 3 | 64 |
| 4 to the power of 4 | 256 |
| 4 to the power of 7 | 16384 |
| seven to the ability of 3 | 343 |
| 12 to the second power | 144 |
| two.5 to the ability of 3 | xv.625 |
| 12 to the power of 3 | 1728 |
| 10 exponent 3 | grand |
| 24 to the second power (242) | 576 |
| 10 to the power of 3 | grand |
| 3 to the power of v | 243 |
| 6 to the power of 3 | 216 |
| 9 to the power of iii | 729 |
| 9 to the ability of ii | 81 |
| 10 to the power of five | 100000 |
Exponent Rules:
Learning the exponent rules along with log rules can make maths really easy for understanding. There are 7 exponent rules.
- Cipher Holding of exponent:
It means if the power of a base is zero then the value of the solution will be 1.
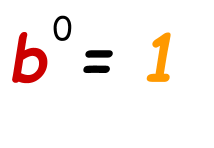
Example: Simplify five0.
In this question, the power of base is cipher, and so according to the zip property of exponents, the answer of this non null base is 1. Hence,
50= 1
- Negative Property of exponent:
It means when the power of base is a negative number, then after multiplying nosotros volition have to find the reciprocal of the respond.
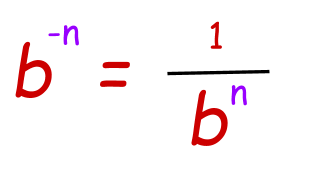
Instance: Simplify 1/three-ii.
We will first make the power positive by taking reciprocal.
ane/3-2=iii2
32 = ix
- Product Property of exponent:
When ii exponential expressions having the aforementioned non zero base and different powers are multiplied, then their powers are added over the same base.
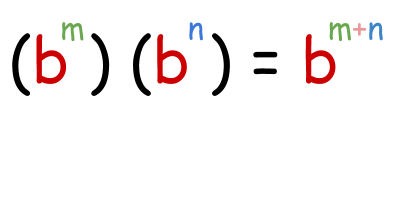
Case: Solve (26)(2ii).
As it is obvious, bases are the same so powers are to be added. Now
(26)(22) = iivi+two
twoviii =ii*2*2*ii*ii*ii*2*2
=256
- Quotient Property of exponent:
It is the opposite of the product property of exponent. When 2 aforementioned bases having different exponents are required to be divided, then their powers are subtracted.
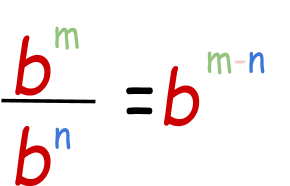
Instance: Simplify 37 /32
iii7/ threeii=37-ii
35=3*3*three*iii*3
= 243
- Power of a Power Property:
When an exponent expression further has ability, so firstly y'all need to multiply the powers and then solve the expression.

Example: Solve: ( ten2)3.
Keeping in view the power of power property of exponents, we will multiply powers.
(x2)3=xtwo*3
= x6
- Power of a production holding:
When a product of bases is raised to some power, the bases will possess the power separately.
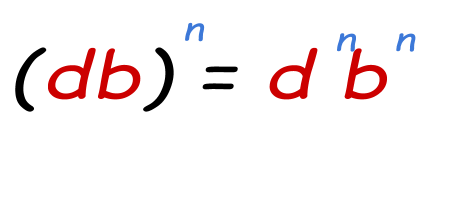
Example: Simplify (4*5)2
iv ii * 5 2 =16* 25
= 400
- Ability of a Quotient Property:
It is the same as the power of a production property. Ability belongs separately to both the numerator and denominator.
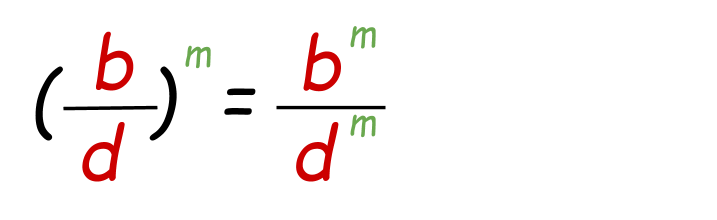
Case: Solve (2/3)two
(2/three)two=two2 / 32
22/ threetwo=4/ix
Source: https://www.meracalculator.com/math/exponents.php
0 Response to "What Is 5 to the Power of 0"
Enviar um comentário